Trong hình học, tứ giác nội tiếp là một khái niệm rất quan trọng và được áp dụng nhiều trong các bài toán chứng minh. Tứ giác nội tiếp là một tứ giác có bốn đỉnh nằm trên một đường tròn, và đường tròn này được gọi là đường tròn ngoại tiếp tứ giác. Trong bài viết này, chúng ta sẽ tìm hiểu về tính chất, dấu hiệu nhận biết và cách chứng minh tứ giác nội tiếp.
Tứ giác nội tiếp là gì?
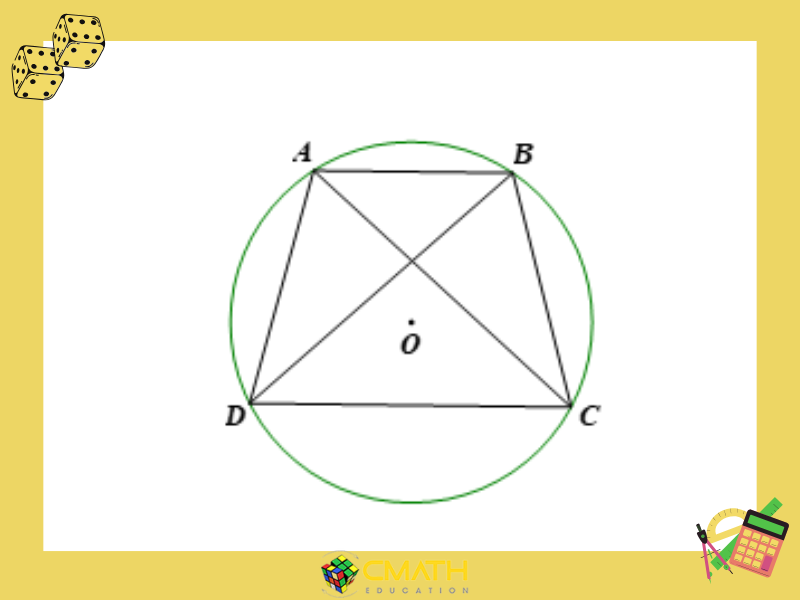
Tứ giác nội tiếp là một tứ giác có bốn đỉnh nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp tứ giác. Tứ giác nội tiếp có tính chất đặc biệt mà chúng ta sẽ đề cập trong phần tiếp theo.
Tính chất của tứ giác nội tiếp
Tứ giác nội tiếp có một số tính chất đặc biệt mà bạn cần nhớ khi làm bài toán hình học. Những tính chất này không chỉ giúp bạn nhận diện tứ giác nội tiếp mà còn giúp chứng minh các yếu tố liên quan.
Tính chất 1: tổng hai góc đối diện bằng 180°
Một trong những tính chất quan trọng nhất của tứ giác nội tiếp là tổng số đo hai góc đối diện bằng 180°. Nếu bạn gặp một tứ giác mà tổng của hai góc đối diện bằng 180°, thì tứ giác đó chắc chắn nội tiếp một đường tròn.
Tính chất 2: nếu tổng hai góc đối diện bằng 180°, tứ giác nội tiếp được đường tròn
Ngược lại, nếu một tứ giác có tổng số đo của hai góc đối diện bằng 180°, thì tứ giác đó có thể nội tiếp một đường tròn. Đây là điều kiện cần thiết và đủ để chứng minh tứ giác là nội tiếp.
Dấu hiệu nhận biết tứ giác nội tiếp
Để nhận biết một tứ giác có phải là tứ giác nội tiếp hay không, ta có thể dựa vào một số dấu hiệu sau:
Dấu hiệu 1: tổng hai góc đối diện bằng 180°
Nếu tổng số đo của hai góc đối diện trong tứ giác là 180°, thì tứ giác đó nội tiếp một đường tròn.
Dấu hiệu 2: góc ngoài và góc trong đối diện bằng nhau
Tứ giác nội tiếp cũng có dấu hiệu đặc biệt: góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện. Đây là một dấu hiệu quan trọng để xác định tứ giác có phải là tứ giác nội tiếp hay không.
Dấu hiệu 3: bốn đỉnh cách đều một điểm
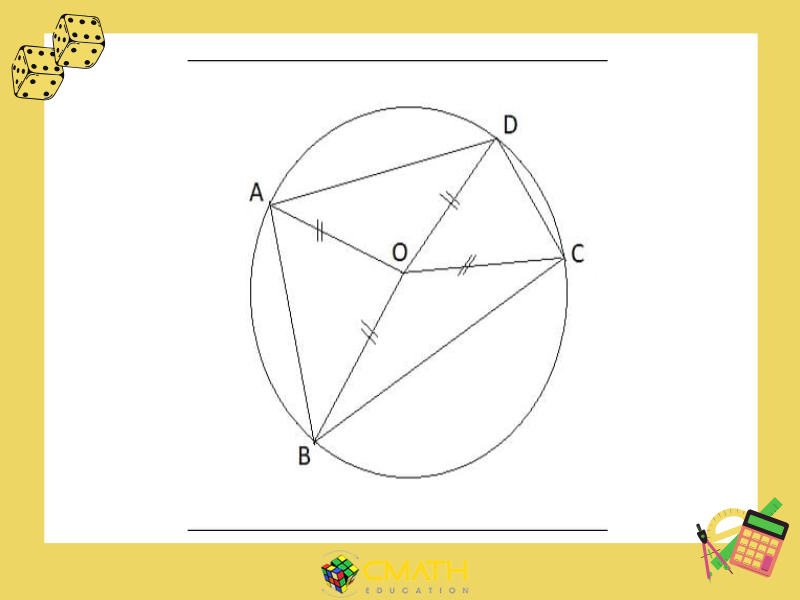
Tứ giác nội tiếp có bốn đỉnh cách đều một điểm cố định, điểm này chính là tâm của đường tròn ngoại tiếp tứ giác.
Dấu hiệu 4: góc tại các đỉnh liền kề
Tứ giác nội tiếp còn có dấu hiệu đặc biệt khi hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc. Nếu bạn gặp tứ giác có đặc điểm này, thì đây là một tứ giác nội tiếp.
Trong các hình học đã học, những hình như hình chữ nhật, hình vuông và hình thang cân đều là các tứ giác nội tiếp.
Bài tập về tứ giác nội tiếp
Tứ giác nội tiếp là một nội dung quan trọng trong chương trình toán học lớp 9, đặc biệt khi học về các tính chất và dấu hiệu nhận biết tứ giác nội tiếp. Sau đây là các dạng bài tập phổ biến mà bạn có thể gặp khi giải quyết các bài toán hình học với tứ giác nội tiếp.
Dạng Bài 1: Chứng minh tứ giác nội tiếp
Một dạng bài tập thường gặp là chứng minh tứ giác nội tiếp trong một đường tròn. Để giải dạng bài này, bạn có thể áp dụng một số phương pháp sau:
Cách 1: Chứng minh tổng hai góc đối diện bằng 180°
Phương pháp này được sử dụng nhiều nhất. Nếu bạn chứng minh rằng tổng của hai góc đối diện của tứ giác là 180°, thì bạn có thể kết luận rằng tứ giác này nội tiếp một đường tròn.
Cách 2: Chứng minh hai đỉnh liền kề cùng nhìn về một cạnh chung
Nếu hai đỉnh liền kề của tứ giác nhìn về một cạnh chung dưới cùng một góc, thì tứ giác đó nội tiếp được một đường tròn.
Cách 3: Chứng minh góc ngoài bằng góc trong đối diện
Bạn cũng có thể chứng minh rằng tứ giác nội tiếp nếu có một góc ngoài tại một đỉnh bằng với góc trong tại đỉnh đối diện.
Cách 4: Chứng minh có một điểm cách đều các đỉnh
Chứng minh rằng có một điểm cách đều bốn đỉnh của hình thì đó là tâm của đường tròn ngoại tiếp, từ đó suy ra rằng hình này nội tiếp.
Dạng bài 2: Sử dụng tứ giác nội tiếp để chứng minh góc, đoạn thẳng, đường thẳng
Các bài toán liên quan đến tứ giác nội tiếp thường yêu cầu bạn sử dụng các tính chất đặc biệt của nó, bao gồm:
- Tổng hai góc đối diện bằng 180°.
- Góc nội tiếp bằng nửa góc ở tâm chắn cùng một cung.
- Các đoạn thẳng liên quan đến tâm của đường tròn ngoại tiếp.
Các bài tập này không chỉ giúp bạn rèn luyện kỹ năng tư duy logic mà còn củng cố các kiến thức về tính chất và dấu hiệu nhận biết tứ giác nội tiếp.
Tứ giác nội tiếp là một khái niệm quan trọng trong hình học, với nhiều tính chất đặc biệt như tổng hai góc đối diện bằng 180° và có khả năng nội tiếp trong một đường tròn. Việc nhận biết và chứng minh tứ giác nội tiếp giúp bạn giải quyết nhiều bài toán hình học thú vị và hữu ích. Nhớ rằng những hình như hình vuông, hình chữ nhật, hình thang cân đều là các ví dụ của tứ giác nội tiếp đường tròn.