Trong hình học, trục đối xứng là một khái niệm rất quan trọng. Nó giúp ta hiểu được cách các hình học có thể chia đôi sao cho hai phần bên trái và bên phải hoàn toàn giống nhau. Cùng tìm hiểu trục đối xứng là gì và các loại hình có trục đối xứng, đặc biệt là hình thang cân.
Trục đối xứng là gì?
Trục đối xứng là một đường thẳng chia một hình học thành hai phần đối xứng với nhau. Nói cách khác, nếu bạn gấp hình qua trục đối xứng, thì hai nửa của hình đó sẽ khớp với nhau hoàn hảo, giống như một sự phản chiếu.
Tính chất của trục đối xứng
Phép đối xứng trục không chỉ giúp chúng ta hiểu rõ về tính chất đối xứng của hình học, mà còn có một số tính chất quan trọng mà học sinh cần nắm vững:
- Bảo toàn khoảng cách: Khoảng cách giữa hai điểm bất kỳ không thay đổi sau khi thực hiện phép đối xứng.
- Biến đường thẳng thành đường thẳng: Đoạn thẳng được biến thành một đoạn thẳng có độ dài và hướng giống như đoạn thẳng ban đầu.
- Bảo toàn góc: Góc giữa hai đường thẳng không thay đổi sau phép đối xứng.
- Hai hình đối xứng nhau qua một đường thẳng thì bằng nhau: Khi hai hình đối xứng qua trục, chúng có đầy đủ các tính chất giống nhau.
Các loại hình có trục đối xứng
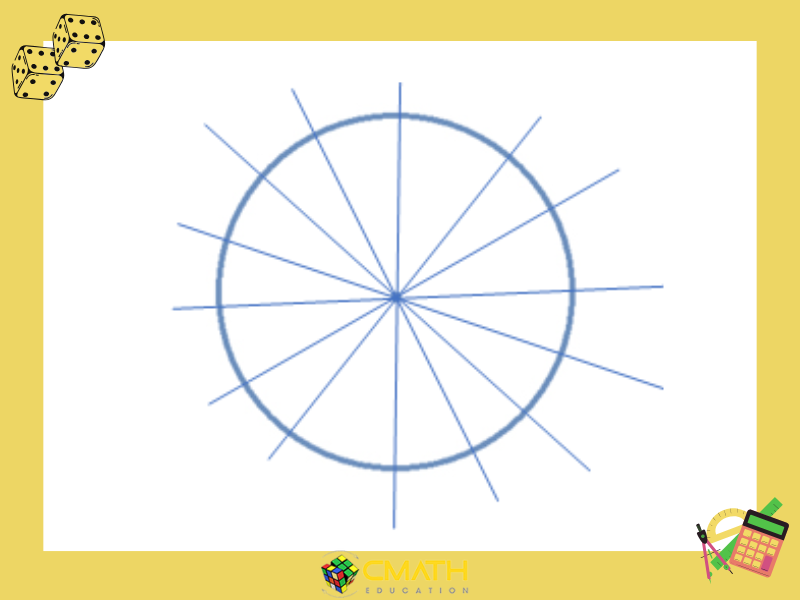
Đường Tròn
Đường tròn là hình có vô số trục đối xứng, điều này có nghĩa là mọi đường thẳng đi qua tâm của đường tròn đều là một trục đối xứng. Do có vô hạn các đường thẳng đi qua tâm, nên hình tròn có số lượng trục đối xứng vô hạn.
Tính chất:
- Mỗi đường thẳng đi qua tâm đều chia đường tròn thành hai phần đối xứng.
- Trục đối xứng có thể là bất kỳ đường kính nào của hình tròn.
Các loại tam giác có trục đối xứng
Tam Giác Cân
Tam giác cân có 1 trục đối xứng duy nhất. Trục đối xứng này là đường thẳng đi qua đỉnh góc cân và trung điểm của cạnh đáy. Đặc biệt, trục này cũng chính là:
- Đường cao
- Đường phân giác
- Đường trung tuyến
- Đường trung trực xuất phát từ đỉnh
Tam giác đều
Tam giác đều có 3 trục đối xứng, mỗi trục đi qua một đỉnh và trung điểm của cạnh đối diện. Các trục này không chỉ là trục đối xứng mà còn là:
- Đường cao
- Đường phân giác
- Đường trung tuyến
Các tứ giác đặc biệt có trục đối xứng
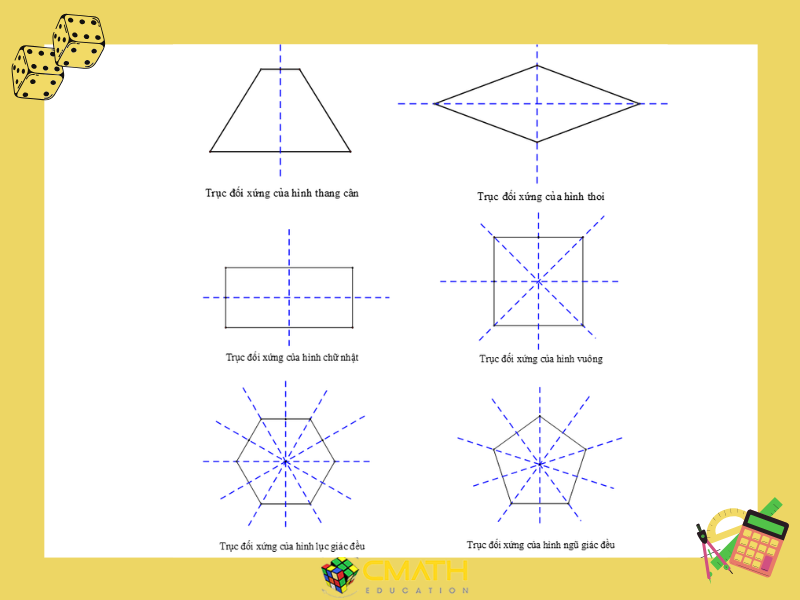
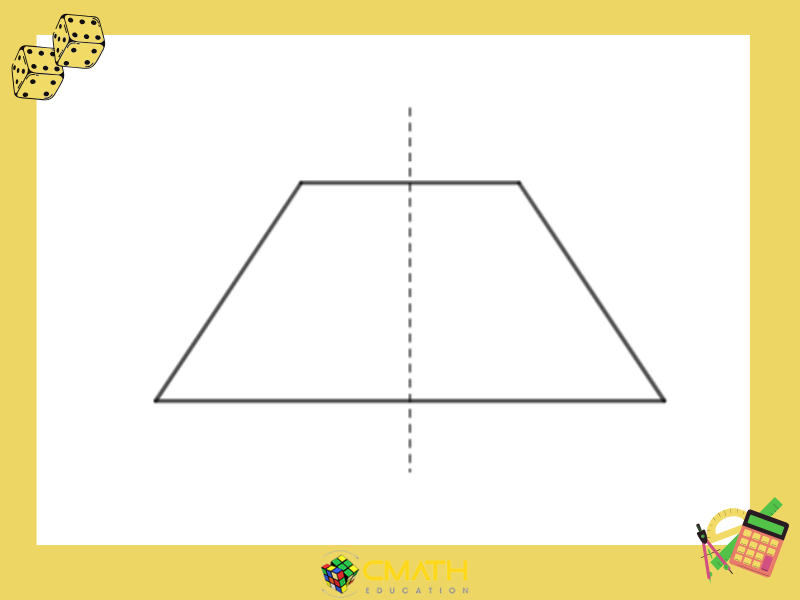
Hình Thang Cân
Hình thang cân có 1 trục đối xứng, đường thẳng này đi qua trung điểm của hai đáy. Đây là một tính chất quan trọng trong hình học lớp 8 và là đặc điểm giúp phân biệt hình thang cân với các hình thang thông thường.
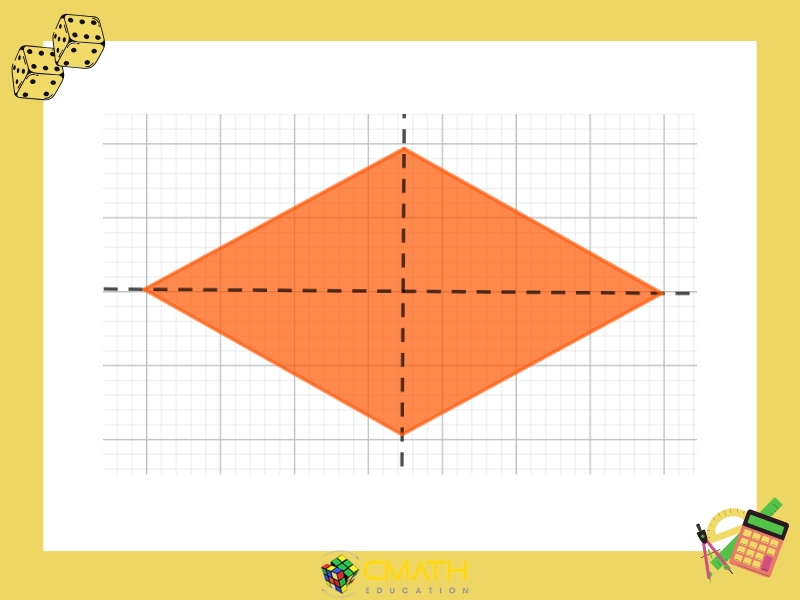
Hình Thoi
Hình thoi có 2 trục đối xứng, đó là hai đường chéo của hình thoi. Mỗi đường chéo chia hình thoi thành hai phần đối xứng qua chúng.
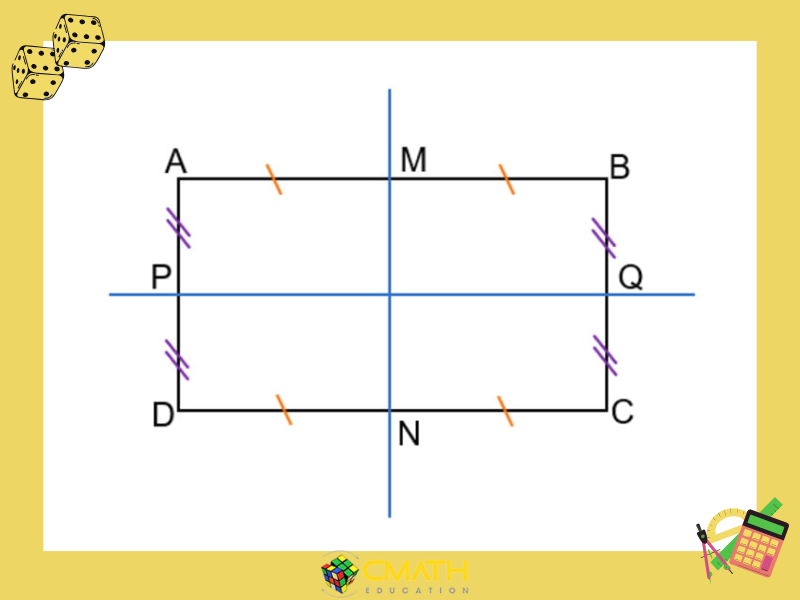
Hình Chữ Nhật
Hình chữ nhật có 2 trục đối xứng, các trục này là các đường thẳng đi qua trung điểm của mỗi cặp cạnh đối diện.
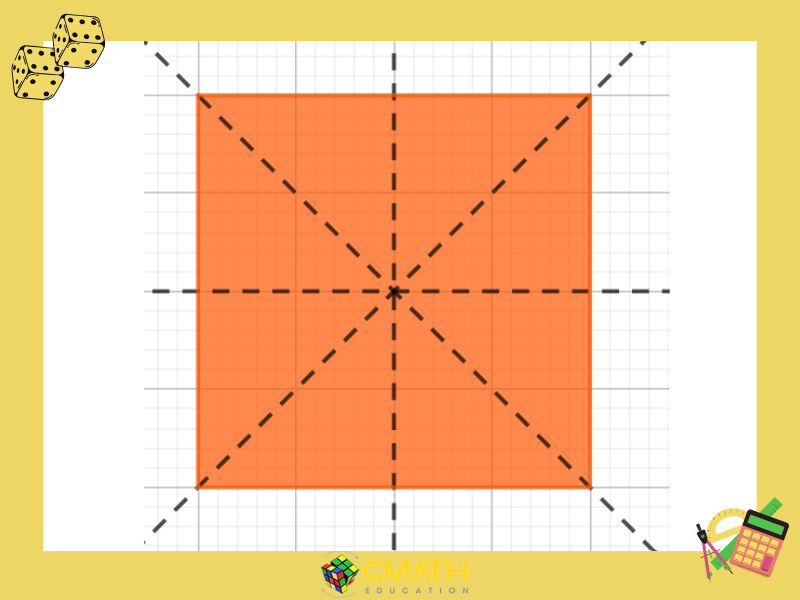
Hình Vuông
Hình vuông là hình có 4 trục đối xứng. Các trục này bao gồm:
- Hai đường chéo
- Hai đường thẳng đi qua trung điểm của mỗi cặp cạnh đối diện
Đa giác đều có trục đối xứng
Một quy luật quan trọng trong hình học là đa giác đều có n trục đối xứng, trong đó n là số cạnh của đa giác. Ví dụ:
- Hình ngũ giác đều có 5 trục đối xứng.
- Hình lục giác đều có 6 trục đối xứng.
Mỗi trục đối xứng của đa giác đều đi qua một đỉnh và trung điểm của cạnh đối diện.
Ứng dụng thực tế của trục đối xứng
Trục đối xứng không chỉ là một khái niệm trong sách giáo khoa mà còn có mặt trong rất nhiều lĩnh vực trong cuộc sống hàng ngày. Cùng khám phá một số ứng dụng thực tế:
Kiến trúc
Trong kiến trúc, các tòa nhà, đền chùa, và công trình nghệ thuật thường được thiết kế theo nguyên tắc đối xứng để tạo ra sự cân đối và hài hòa.
Thiết kế
Nhiều logo, biểu tượng và sản phẩm thiết kế sử dụng tính đối xứng để tạo ra một ấn tượng mạnh mẽ với người nhìn, mang lại cảm giác cân bằng và đẹp mắt.
Tự nhiên
Trong tự nhiên, tính đối xứng xuất hiện ở lá cây, cánh bướm, và khuôn mặt con người. Sự đối xứng giúp các sinh vật duy trì sự hài hòa và cân bằng trong cấu trúc cơ thể.
Hình thang cân có mấy hình đối xứng?
Hình thang cân là một loại hình thang có tính đối xứng đặc biệt. Trong hình thang cân, trục đối xứng chính là đường trung trực của đáy lớn, chia hình thang thành hai phần giống hệt nhau.
Đặc điểm của trục đối xứng hình thang cân
- Đường trung trực của đáy lớn: Trục đối xứng của hình thang cân luôn là đường thẳng vuông góc với hai đáy, đi qua trung điểm của đáy lớn.
- Góc đối xứng: Các góc kề một đáy trong hình thang cân sẽ bằng nhau và đối xứng qua trục đối xứng.
- Đường chéo đối xứng: Hai đường chéo của hình thang cân cũng cắt nhau tại điểm trung bình của mỗi cạnh đáy.
Mỗi hình thang cân chỉ có một trục đối xứng
Vì hình thang cân có đối xứng qua đường trung trực của đáy lớn, nên chỉ có một trục đối xứng duy nhất, điều này phân biệt nó với các hình như hình vuông, hình chữ nhật hay hình tròn.
Trục đối xứng là một khái niệm quan trọng trong hình học, đặc biệt trong các bài toán liên quan đến đối xứng của hình học. Hình thang cân là một hình đặc biệt có một trục đối xứng, chia hình thang thành hai phần đối xứng qua trục trung trực của đáy lớn. Các loại hình khác như hình vuông, hình chữ nhật và hình tròn cũng có trục đối xứng, giúp chúng ta dễ dàng nhận diện và áp dụng trong các bài toán hình học.